Control Moderna" de Katsuhijo Ogata. Mi ejercicio fue el siguiente:
Para h(t) no es necesario encontrar la función de alguna forma en específico, basta con ver la gráfica para saber que h(t) siempre será igual a T, desde T hasta infinito. Pero g(t) es diferente(aunque sería fácil deducir también de manera gráfica que g(t) = t, explicaré como obtenerla). Para obtener g(t), utilizamos dos puntos de la gráfica(1) para luego sustituirlos en la ecuación(2):
(1) (2)
Entonces lo restante es sustituir los valores de los puntos en la ecuación, y despejar y. Lo cual se hace así:
Ya que tenemos g(t) y h(t), podemos proceder a encontrar la transformada de Laplace. Para esto utilizamos la fórmula que dice:
Pero nosotros no tenemos una función directa f(t), tenemos las dos funciones que forman f(t): g(t) y h(t), por lo tanto, partimos los intervalos de ésta fórmula en dos (de 0 a T, y de T a infinito, como g(t) y h(t)). Después sustituimos g(t) y h(t). La fórmula entonces quedaría así:
Entonces para encontrar la Transformada de Laplace de f(t) debemos integrar ambas partes. Para comprender más fácilmente ésto, lo haré por partes, integrando primero (1) y luego (2), al final entonces simplemente las sumaríamos. También ignoraré los intervalos por ahora, más adelante los evaluamos.
Para integrar (1) tenemos que realizarlo por partes; si no sabemos como, se utiliza la fórmula:
Entonces sustituyendo los valores, e integrando quedaría algo así:
(Nota: no voy a explicar paso a paso las integrales porque es algo tedioso, solo me dedicaré a explicar superficialmente)
Eso es para el primer intervalo, para el segundo, que sería la ecuación (2), la integral es bastante sencilla:
(T es constante, por lo tanto podemos sacarla de la integral)
Ya teniendo ambas integrales, debemos ahora sí evaluarlas en los intervalos correspondientes.
Con evaluarlas me refiero a sustituir los valores de los extremos de los intervalos superior e inferior, y restarlos respectivamente. Entonces, volvemos a separar ambas en (1) y (2) para entenderlo más fácilmente. Para evaluar (1) y (2) entonces tenemos que:
Ahora estos valores serán los que sumaremos para obtener finalmente la transformada de Laplace, de la siguiente manera:
Pero aún así podemos simplificarla un poco más, agrupando los términos que tienen s^2 de denominador. Quedando definitivamente de la siguiente forma:
Resultado:
Y este fue el ejercicio de la Tarea 2, tengo que decir que no fue sencillo, debido a que no recordaba bien como realizar este tipo de ejercicios(el problema estaba sencillo).
Referencia:






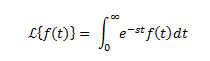



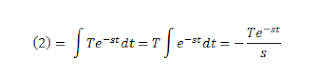





Bien; 15 pts.
ResponderEliminar