Adaptive Coding

For this week, I had to "invent", implement and evaluate my own adaptive coding method. I say 'invent' because probably the way I did it already exists, and is not the most optimal way.

Design

The huffman coding method normally is an offline compressor, because it works with the whole text beforehand and generates the tree based on the character's frequencies. But in the case of an adaptive coding we cannot do that because the compression is going to be online, ergo, the text is going to be received character by character, ant the purpose of making it adaptive is to generate the code as the character is received.

The way I did it is to build a Tree beforehand. This tree technically can be as simple as the whole alphabet with random frequencies, or just the alphabet disordered in the tree's nodes without caring about the frequencies. But I did not wanted to do it just like that. So what I did was to build the tree using known frequencies of the english language. Of course, this would just work when the text to compress is in english, but it works for simple cases.

With this we can build a decent tree before the online compression begins. But the problem now is that the text can and probably will have new characters that weren't considered when the tree was built.

So for this cases after the tree is complete a 'dummy' character is added with 0 frequency ('dummy' is a word not a character I know, but I can't just use any character for this purpose because it can be included in the text). This 'dummy' will work as a placeholder, separating space for a new character that is found on the text, which also works because if a new character is found, we can assume that this character which was not included in the tree-building process is not going to be very frequent character, so adding it in that space is not that bad.

But that's not it, the new character can't just replace the 'dummy' because if another new character came then it would not have space in the tree. So every time a new character comes, we search for the actual 'dummy' who is a leaf of the tree, add two child nodes which will be the new character, and another 'dummy'. This way there would be more space if another new character comes.

This process is not going to affect the already generated codes, because the new modifications to the tree are made at the same spot.

Code




Distribution file



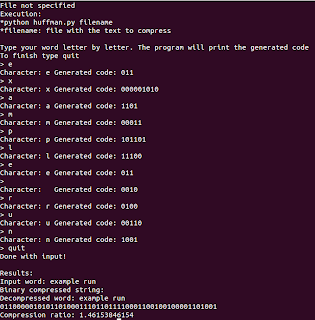
Example run:

Reading character by character:

Reading text from file:

Performance

To test the performance of the algorithm, like in the case of the Huffman Coding I measured the compression ratio and the time it takes to compress. The text used was the Python's Zen:

"The Zen of Python, by Tim Peters

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!"

To test the time and compression ratio, I measured both reading different lengths of the previous text.

The graphics plotted from the data:

The time graphic doesn't reveal too much about the algorithm, because as expected it increases in time as the length of the text increases. It is worth noting anyway that the time it takes to compress a 900 character text is 2 seconds, which is not very good, considering that the standard Huffman coding could do much better.

Now this graphic clearly reveals the nature of the algorithm. Initially, the compression ratio starts bad, as there is few characters and the first of them are new, so the generated codes are large, making the compression a expansion. But as the length increases, the graphic stabilizes because it starts to read common letters that are already in the buffer because of the initialization process. The following drops or inferior peaks are created every time a new character appears, because a large code is generated for them. 

As the text length increases, the algorithm is more stable, because it has a nice buffer to work with. That said the compression ratio is not very good, but at least it doesn't expand the size.

Future improvement

Some considerations with this algorithm is that, as I mentioned earlier, it only would work acceptable with texts in a known language, and that assuming that we know the distribution of letter's frequencies in that language so a initial setup can be done.

Another thing is the fact that although the 'dummy' replacement process works fine making the algorithm adaptive, this is far beyond optimal assuming that we will get a lot of new characters, because  every new character added to a 'dummy' space increases the length of the generated code by 1. So the growth of the code as new characters appear (and therefore the downfall of the compression ratio) is $ O ( n^2)$.

With that said, future improvement to this algorithm would be:

• Multiple distributions: Assuming that we are going to compress just normal text in several languages, having multiple files with distribution of letter's frequencies in different languages could help improve the compression rate just selecting the language in which the text is written. Or a possible general distribution, but this is a lot harder.
• A more complete distribution: Also continuing with the distribution problem, the one that I used only contained the alphabet letters, and even so it didn't discriminate between lower case and upper case. So a more general distribution, but in this case with more characters would also be a good initialization idea.
• Dynamic 'dummy' spacing. Instead of having just one 'dummy' space which is going to span a lot of more 'dummies' as new characters appear, having more or changing the space where they are added when a certain peak is reached would improve the compression rate in cases where a lot of new characters are found.