For the second assignment, I was tasked to do some sort of analysis for my one-time-pad program that I did for the previous assignment, and with that hack it. I don't think I can actually hack the program, because even if the random numbers that python's randint function uses aren't totally random(of course they aren't) I can't seem to think of a way to predict them or figure a pattern.
Character Frequency Test
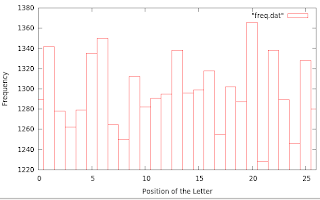
First, I did a simple frequency test, to see which letters were generated the most for the key. I have to say that my keys were generated using randint in a reduced range for all the letters of the alphabet(in lowercase) and also the space character. So it would be something like randint(0, 28).
With that said, I just wanted to get a frequency of the letters, which would also be the frequency of the numbers, to see how many times some characters were repeated. Of course this doesn't tell much, because as we can see on the graphic, the frequency of each number, even though it is different, it is not a huge difference so we can't tell if there's a pattern at all.
Frequency Monobit Test
To test the proportion of ones and zeros in order to find if there are many zeros or many ones, the monobit test is useful. The puropose is to find if the number of zeros and ones is approximately the same, as expected in a random sequence. I already had done this in a previous class, so I just had to adapt a little the code to my current one-time-pad key generator, but a better explanation to the monobit test can be found here(in spanish).
def frequency_test(lista):
suma = 0
lista = list(lista)
n = len(lista)
for i in range(len(lista)):
if lista[i] == "0":
suma += -1
else:
suma += 1
suma_abs = abs(suma)/math.sqrt(n)
p_value = math.erfc(suma_abs/math.sqrt(2))
if p_value < 0.01:
print "Frequency Test: Not passed\n"
else:
print "Frequency Test: Passed\n"
The test produced the next results:
The p value, which is used to determine if the test is passed or not, was bellow 0.01, which means the test didn't passed, so our random generator doesn't generate a good enough proportion of random zeros and ones. I think generating the bits of the key one by one, using an uniform distribution would help in improving this, because the number of ones and zeros would be more proportioal.
Searching for a Graphical Pattern in a Bitmap
An easy way to tell if a random generator is just plain dumb, is to look at the patterns it can generate in a graphical way. For example, this image taken from RANDOM.ORG is a bitmap of the PHP rand function on Windows:
PHP rand in Windows
As we can see, there is a clear graphical pattern, so we can tell that is not really random. Now i tried to do the same with the python random generator, using Tkinter to draw small dots using the line widget. I move between every coordinate in an area, and I draw a dot if a random generated number is 1, or I don't if it is 0. The simple python script I used:
#!/usr/bin/python
from Tkinter import *
from random import randint
master = Tk()
w = Canvas(master, width=700, height=700, background="white")
w.pack()
for i in range(700):
for j in range(700):
if randint(0, 1) == 1:
w.create_line(i, j, i+1, j+1)
mainloop()
The result was this:
Python's random in Linux
I personally can't see a visual pattern here, so I assume this is a pretty good random generator, so I call this test passed.
Chi2 test
Using the chisquare function of the scipy library, it is possible to do the chisquare test to an array of frequencies. For this, I used the frequencies of the first test, and the simple code is the following:
#!/usr/bin/python
from random import randint
import numpy
import scipy.stats
alphabet = "abcdefghijklmnopqrstuvwxyz "
def generate_key(size):
key = ""
for i in range(size):
key += alphabet[randint(0, len(alphabet)-1)]
return key
def zeros(size):
array = []
for i in range(size):
array.append(0)
return array
def frequency_test(key):
freq = zeros(len(key))
for i in range(len(key)):
for j in range(len(key)):
if key[i] == key[j]:
freq[i]+=1
return freq
def expected(size):
box_size = size/len(alphabet)
freq_exp = zeros(size)
for i in range(size):
freq_exp[i] = box_size
return freq_exp
freq_obs = frequency_test(generate_key(100))
freq_exp = expected(len(freq_obs))
array_obs = numpy.array(freq_obs)
array_exp = numpy.array(freq_exp)
print "Observable Frequencies(Random Numbers frequencies): %s\n"%array_obs
print "Expected Frequencies: %s"%array_exp
chi_stat, p_value = scipy.stats.chisquare(array_obs, array_exp)
print "Chi2 Statistic: %s"%chi_stat
print "P Value Statistic: %s"%p_value
The function scipy.stats.chisquare(f_obs, f_exp=None, ddof=0) generates two values, the chisquare test statistic, and the p-value, used to check if the test was passed or not.
The parameters are:
- f_obs : array
- observed frequencies in each category
- f_exp : array, optional
- expected frequencies in each category. By default the categories are assumed to be equally likely.
- ddof : int, optional
- adjustment to the degrees of freedom for the p-value
To get the observed frequencies, like I said I use the first frequency test to get which letters, or random numbers are repeated and how much time, and I fill a list of the respective frequencies. For the expected frequencies, I generated a list of frequencies, but these frequencies are as we would expect to be, so I divided the size of the random samples (the size of the alphabet used to generate keys) between the size of the key, so I could fill boxes with the same frequencies, as expected from a uniform random generator.
Then giving these two parameters to the function, I got a p_value, and a chisquare statistic. The p value just like the monobit test, help us to determine if the test was passed or not. In this case the test never passed:
Things to get my One-Time-Pad better
First of all, I fixed some minor things that my one time pad:
- My one-time-pad generated one key per word of the message, which at the end wouldn't be much different from the regular results, but it wasn't the best approach.
- My one-time-pad used to skip spaces, not encrypting them. So, now I added the spaces to the alphabet array, so it can be encrypted along with the message.
- My one-time-pad wasn't modular. It used to be sequential, doing a lot of things in the same function, so I separated every important part into its own function, like encrypting, deciphering, generating the key, etc.
Now an important thing that I think would make it better is a file, were all the used keys are stored, this is important, because even though python didn't reuse a single key running the program 10000 times, it is still likely that it will, sometime. So using this file, the program can make sure the generated key is totally new. Of course there is the problem with the reading/wrinting to files, but security comes first.
The code, updated:
from sys import argv, stdout
from random import randint
import math
alphabet = "abcdefghijklmnopqrstuvwxyz "
def letter_pos(letter):
for i in range(len(alphabet)):
if alphabet[i] == letter:
return i
def wiki_cipher(msg, key):
cipher_msg = ""
for i in range(len(msg)):
cipher_msg += alphabet[(letter_pos(msg[i]) + letter_pos(key[i])) % len(alphabet)]
del key
print "Cipher: %s"%cipher_msg
return cipher_msg
def wiki_decipher(cipher_msg, key):
msg = ""
for i in range(len(cipher_msg)):
msg += alphabet[(letter_pos(cipher_msg[i]) - letter_pos(key[i])) % len(alphabet)]
del key
print "Decipher %s"%msg
return msg
def generate_key(size):
key = ""
for i in range(size):
key += alphabet[randint(0, len(alphabet))]
key = key[0:size]
return key
def main():
try:
filename = argv[1]
f = open(filename, "r")
msg = f.readlines()[0]
msg.replace("\n", "")
print "Message:"
print msg
except IndexError as err:
print "File not specified, using default message."
msg = "testing the one time pad encryption"
print "Message: %s"%msg.lower()
key = generate_key(len(msg))
cipher = wiki_cipher(msg, key)
wiki_decipher(cipher, key)
main()
References:







Good. It would have been nice to wrap it all up into a single program that generates a report on the quality of the randomness. That way you could rerun it every time you improve the generation. 7 pts.
ResponderEliminar